Spectral-infinite-element simulation of Gravity and Magnetic data
Ph.D. Project, Queen's University, Canada, 2023
Title: Spectral-infinite-element simulation of Gravity and Magnetic data 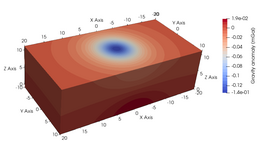 ”
”
Abstract:
In potential field geophysics, imaging techniques are crucial in estimating source property distributions within two- and three-dimensional spaces. Central to this field are the gravity and magnetic methods, which are governed by the unbounded Poisson/Laplace equations. Traditional approaches for solving these equations are based on direct integral methods, where the computational cost is proportional to the number of observational data points. This dependency poses significant challenges in simulating complex models that require higher data points. This study introduces the Spectral-Infinite-Element Method (SIEM) as a potential solution to address these challenges. SIEM uses nodal quadrature to integrate the spectral element method with the mapped infinite element method. Poisson’s equation is solved within the domain of interest using spectral elements in conjunction with the Gauss-Legendre-Lobatto (GLL) quadrature. For areas outside the domain, the Gauss-Radau quadrature effectively captures the infinite elements in outer space. A distinct advantage of SIEM over traditional integral methods lies in its higher-order discretization capability, which allows for a more accurate representation of complex models. Furthermore, SIEM is independent of the number of observational data points, making it an efficient method for simulating large-scale complex models. The efficacy of SIEM was tested through synthetic simulations of gravity and magnetic methods and compared with analytical solutions. The results demonstrate that SIEM offers a higher accuracy and efficiency over traditional methods. This method provides a robust and scalable solution to complex 3D models with computational ease.
Introduction:
- Potential field geophysics is governed by the unbounded Poisson/Laplace equations
- The traditional direct integral method used to solve this equation poses challenges in computational cost, singularity, scaling with data points, and limiting complex model simulations
- This study introduces the Spectral-Infinite-Element Method (SIEM) as a potential solution to address these challenges
- SIEM combines the spectral element method with mapped infinite elements via nodal quadrature
- Gauss-Legendre-Lobatto and Gauss-Radau quadratures inside and outside the domain, respectively
- SIEM performance is validated against synthetic simulations and analytical solutions
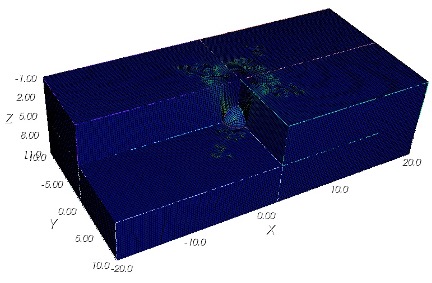
Meshing
A spherical block model was meshed using hexahedral elements, as shown in the figures below.
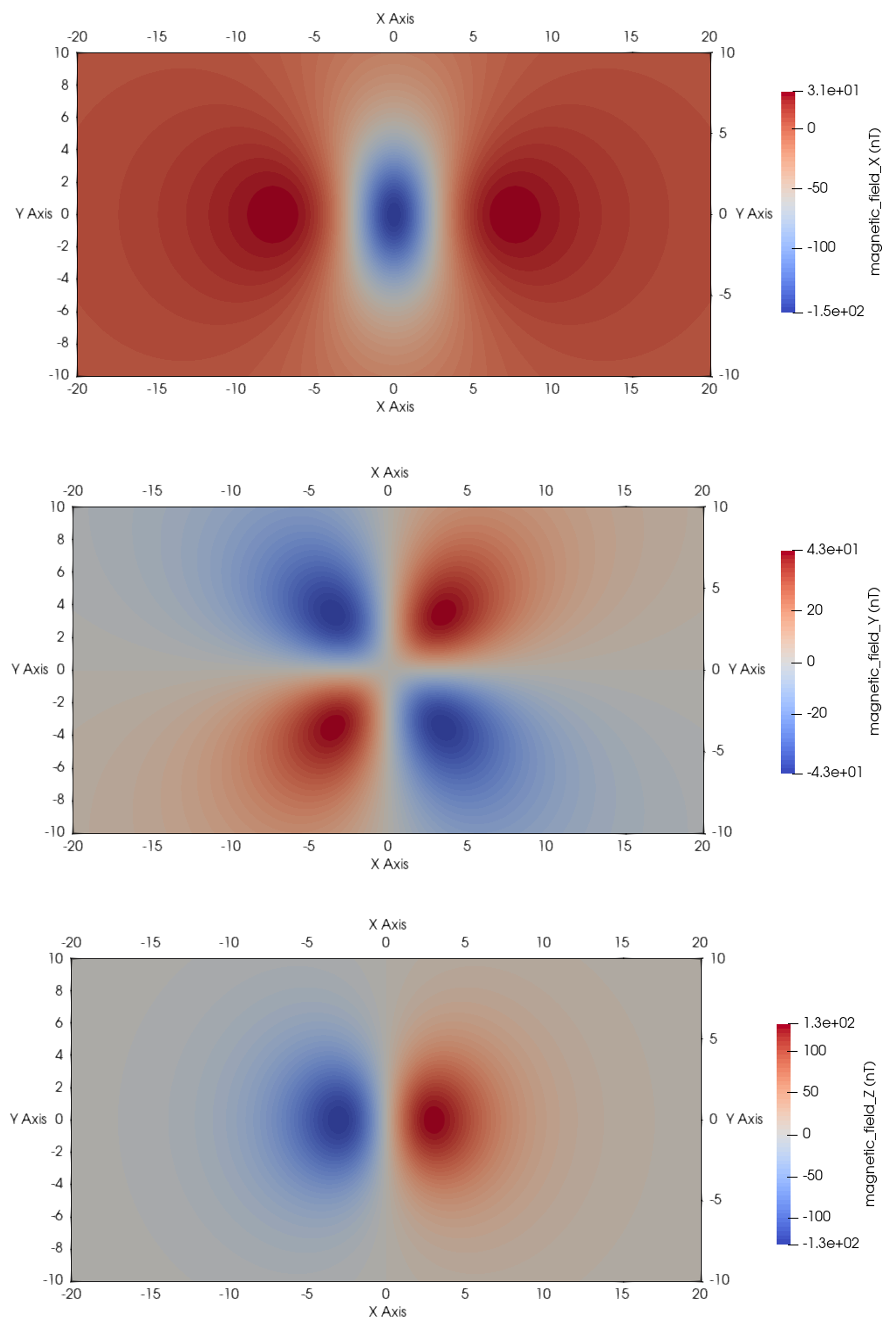
Magnetic Modelling using SPECFEM
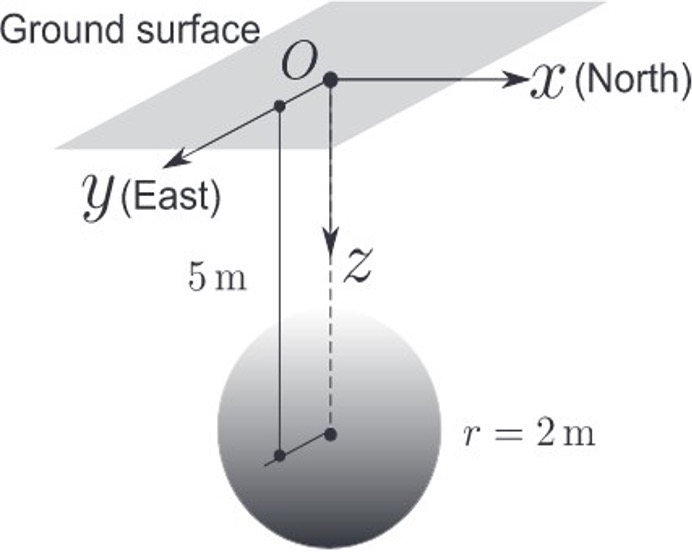
One block model with magnetic intensity \(M = 10 \, \text{Am}^{-1}\), radius \(2 \, \text{m}\), and depth \(5 \, \text{m}\) from the centre is modeled, as illustrated below.
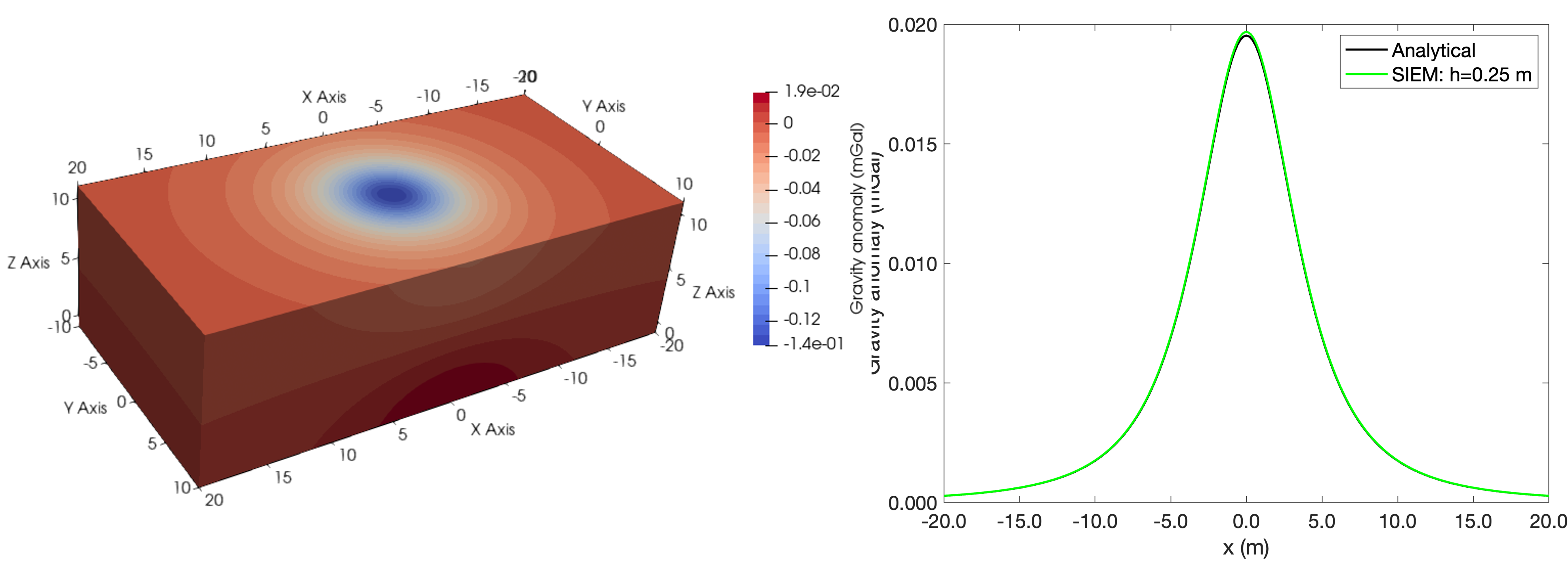
Gravity Modelling using SPECFEM
One block model with density \(\rho = 2200 \, \text{kg/m}^3\), radius \(2 \, \text{m}\), and depth \(5 \, \text{m}\) from the centre.
Summary:
- Independent of observational data points, efficient for large scale models.
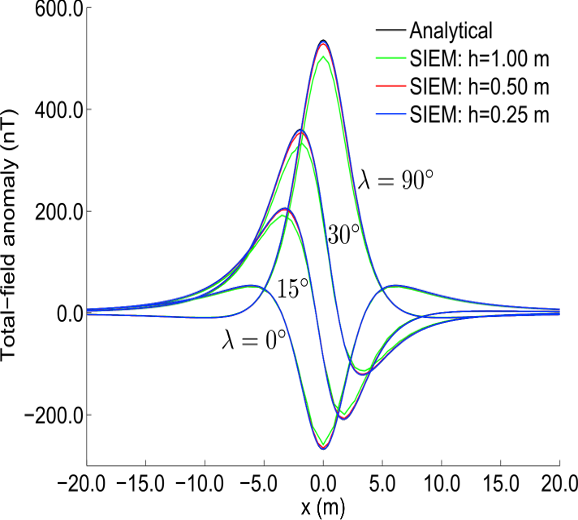
- Resulting anomaly profile close to the analytical solution
- Insensitive to high density/magnetic contrast
- Superior in higher order discretization, enhancing model accuracy
